What makes one's brain a brain? |
Computation in recurrent networks |
Latent space dynamical system models |
Deciphering distributed neural computation |
Deciphering distributed neural computation
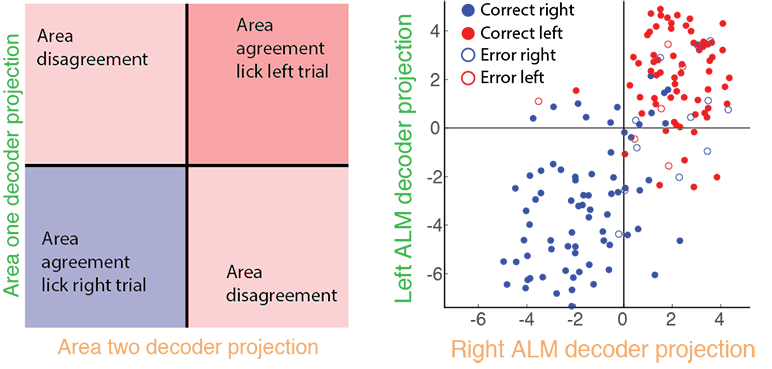
Animals are able to access information regarding the environment even when that information is no longer available to the senses. Such an ability to turn transient sensory stimuli into more stable representations is often referred to as short term memory. When mice are trained to perform such tasks the memory of the stimulus is represented by neural activity in multiple brain areas. These representations are not merely redundant copies of the same information; they dynamically influence each other in ways that potentially improve the task performance. For instance, if one brain area’s representation is corrupted by sensory errors or external perturbations, it can potentially be recovered by other brain areas.
It is natural to hypothesize that neural representations and computations of task-relevant information are broadly distributed generally and not just in these specific tasks. Hence, any description of neural computation for many tasks could be incomplete if it were based on only a single brain area. One of our lab’s main research goals is to understand interactions between distinct brain areas and therefore provide a more complete picture of neural computation in such contexts.
It is natural to hypothesize that neural representations and computations of task-relevant information are broadly distributed generally and not just in these specific tasks. Hence, any description of neural computation for many tasks could be incomplete if it were based on only a single brain area. One of our lab’s main research goals is to understand interactions between distinct brain areas and therefore provide a more complete picture of neural computation in such contexts.
Latent space dynamical system models
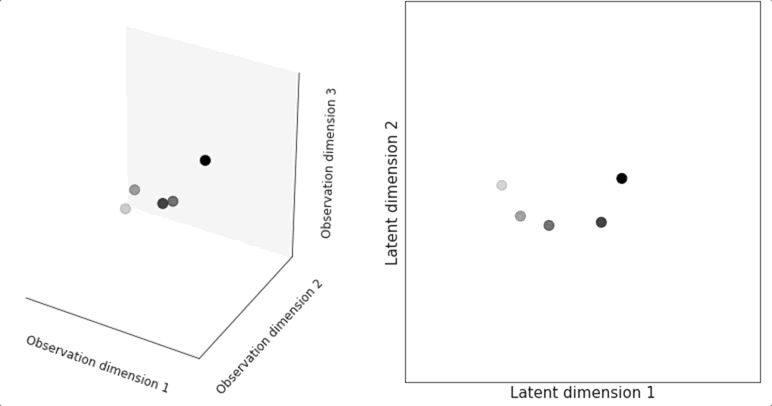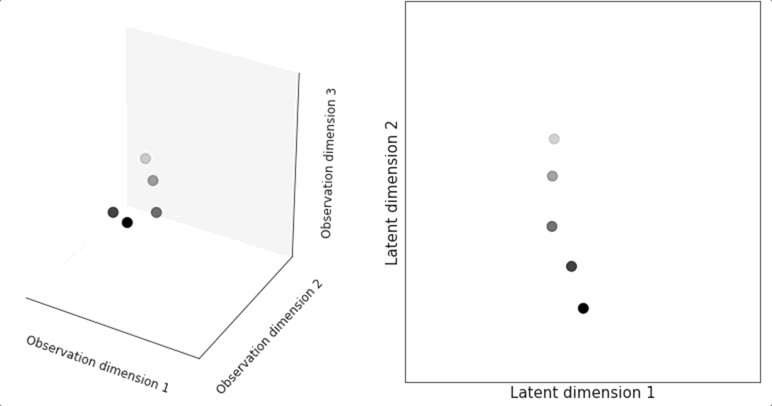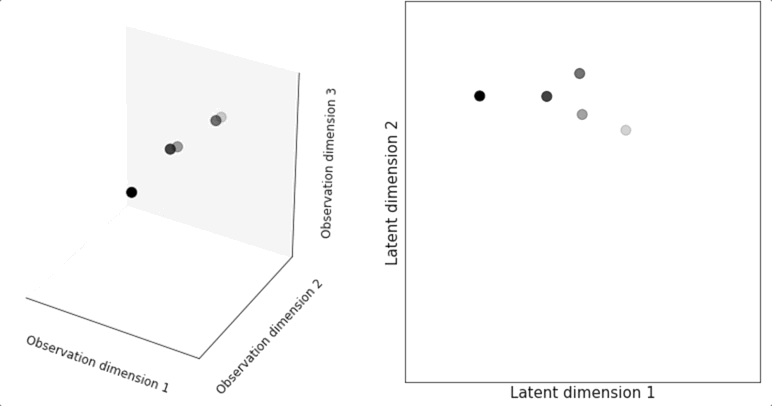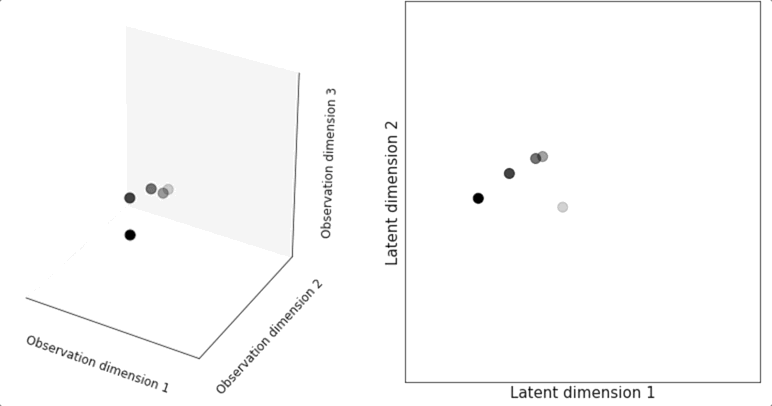
Recent technological advances have given us unprecedented access to the activity of many neurons across both space and time. Yet analyzing this new wealth of data to understand neural population activity can be challenging. Hence, researchers often resort to dimensionality reduction methods that reduce the effective size of our data while retaining important structural features. Most dimensionality reduction techniques are “static” meaning they have no sense of time. That is, if one reshuffles the data with respect to time (e.g. taking the first second of neural activity and making it the tenth second of the shuffled dataset), the answer from a static technique like Principal Component Analysis (PCA) will be exactly the same. Clearly, this is not well matched to analyzing neural data, which has important and strong temporal correlations.
|
(Left) observation of three measurement values from a (hypothetical) system constitute a three dimensional observation space (Right) Dynamics of the observations in an inferred two dimensional latent space.
|
Latent space dynamical systems, in contrast, are a dimensionality reduction approach that explicitly incorporates time. Using a latent space dynamical systems approach, we might model the activity of three neurons as a function of a much simpler, two-dimensional curve moving through our latent space. Intuitively speaking, we choose to assume that the activity is a noisy sample from underlying orderly dynamics. We use the observed data to learn the underlying dynamics and then we de-noise the data by describing the phenomena not by the measured activity itself but rather by the lawful learned trajectory that is closest to the measured data. An added benefit of the dynamical systems approach is that it yields a compact, mathematical description of the population activity that can be used to describe how the underlying dynamics differ across animals, treatments or other factors. In our lab, we use latent dynamical systems to better understand the organization of neural circuits underpinning tasks ranging from chemotaxis to decision-making.
|